在建设制造强国的背景下，机器人作业精密化要求更严苛、控制精度要求更高，尤其对于激光切割和激光焊接等领域。传统的机器人控制策略未考虑其动力学特性，仅在伺服驱动器内部引入PID调节，难以实现高精度运动控制。如何结合机器人的动力学模型，辨识动力学参数且设计高精度运动控制策略，是机器人控制领域的研究热点之一。
本文针对UR5关节型机器人开展研究，首先采用牛顿-拉格朗日法建立机器人动力学模型，并将模型参数进行线性化处理，得到待辨识的最小参数集；其次，为了更好地激励机器人动力学特性，选取有限项傅里叶级数和五阶多项式结合的激励轨迹模型，并以条件数作为优化目标，求解激励轨迹最优参数；然后，利用加权最小二乘法进行机器人动力学参数辨识，并结合验证轨迹评判辨识参数的准确性；最后，根据辨识出的动力学模型，设计前馈控制。仿真结果表明，与PID反馈控制相比，本文提出的前馈补偿控制方法可以提高机器人跟踪精度、加快误差收敛速度，改善机器人动态性能。

关节型机器人动力学建模

关节型机机器人是多输入多输出、非线性和强耦合的系统，建立其动力学模型是进行动力学参数辨识的前提，同时也是设计前馈控制器的基础。本章以UR5机械臂为研究对象，采用牛顿-拉格朗日法进行动力学方程建模，并求解待辨识的最小参数集和回归矩阵，并在simulink建立机械臂运动学和动力学可视化模型。

牛顿-拉格朗日动力学建模

进行动力学建模，需要选取一个计算量合适、编程实现较为容易的建模方法。早期动力学建模主要包括牛顿-欧拉矢量学方法和基于拉格朗日方程的分析力学方法。这两种方法对于自由度较少的简单系统来说，其方程数较少、计算量较小、容易实施。但是对于比较复杂的刚体系统，随着自由度增加，计算量将大幅增加。六关节型机械臂动力学建模采用牛顿-欧拉方法建模虽然计算量较简单，但是拉格朗日方法可以避免刚体内部出现作用力，简化建模过程，因此，本次研究选取牛顿-拉格朗日方法进行动力学建模。拉格朗日建模方法又可以分为直接法和迭代法两种。拉格朗日直接法，在机器人自由度较高时，拉格朗日量计算繁琐，还需要重新组合成为封闭形式的动力学方程。而迭代法充分运用串联机器人特性，直接获得封闭形式动力学方程，编程实现较为便捷，因此，最终选择拉格朗日迭代法。
在实际工业和实际应用中，对机器人关节建模是十分复杂的，会出现非线性等复杂的摩擦因素，且在较低速运动时，摩擦力的影响愈发明显，因此对关节处的摩擦力进行建模也是十分必要。对于零负载以及较低速运行的场景，通常使用库伦-粘滞摩擦模型。为了更好的为实际运作机器人建模，本文考虑摩擦力简化模型。

将摩擦引入后可得机器人动力学非线性模型：

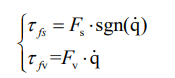
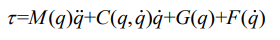
动力学方程参数线性化

机器人动力学参数以一种非线性的方式隐藏在动力学非线性模型中，由于上述表达式参数的非线性，难以辨识得到动力学参数。通过适当的参数重组以及线性变换可将上式转化为：

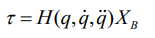
上述表达式可以表示为动力学参数和摩擦参数分离的形式：

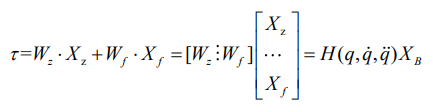
对于机器人的每一段刚体i来说，其基本参数集可以用14个参数来表示动力学特征。

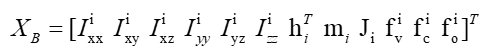
其中各个参数含义如下：

最小参数集和回归矩阵求解

为了减少待辨识参数量，无需对全部的84个参数进行辨识。在已经求解得到完整的线性化机器人动力学模型中，并不是全部的基本动力学参数都可以独立地影响系统的关节力矩值，有一些参数对动力学模型构建不产生影响，另外一些参数以线性组合的形式影响机器人力矩表达式。回归矩阵为零或者线性相关的列，会产生奇点，进一步导致轨迹规划和参数辨识产生问题，在机器人运动过程中，也并非全部的参数都可以辨识得到，因此得到的基本参数矩阵，可以进一步化简为最简参数集。
目前最小参数集求解主要有机器人能量递归方法、QR分解、SVD分解几种方法。QR分解实现起来比较简便，并且不受限于特定约束，因此，本文借助matlab的qr函数直接求解最小参数集。QR函数标准形式：

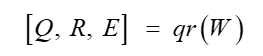
具体函数说明可查阅MATLAB帮助文档。分解完成后，最终需要辨识的参数共计40个以及18个摩擦力参数，他们是基本参数集中的参数或是其线性组合。